For many years, since reading a copy of Human Action loaned to me by a friend who had been a close personal friend of Ludwig von Mises, I have been an amateur devotee of the Austrian School of Economics. My professional life has in one way or another revolved around the subject of fluid dynamics (e.g., this book). These two interests have intersected in the very interesting article by the mathematician Reinhard Siegmund-Schultze called Applied Mathematics versus Fluid Dynamics: The Catalytic Role of Richard von Mises (1883—1953). Of course, Richard is the younger brother of Ludwig. It is fascinating to follow the parallel courses of the two brothers through their respective fields of applied mathematics and economics. Guido Hulsmann alludes to the competitive nature of the von Mises family in his authoritative biography of Ludwig, Mises: The Last Knight of Liberalism. “Like their mother, Ludwig and Richard wrote with a clear and unpretentious style. From childhood they set for themselves the highest standards. And as they developed taste and expertise, they would judge their own achievements and those of others in the light of these standards.” In particular, among their important contributions, both stressed the great importance of the methodological approach employed.
Mises: The Last Knight...
Buy New $4.95
(as of 11:50 UTC - Details)
In my understanding, Ludwig forcefully contended that economics should rest on the neo-Kantian principles of a priori understanding and from this he logically built an edifice of economic understanding of the real world. He continually fought against the empirical German Historical School. As Hulsmann quotes in Last Knight:
I was still in high school when I noticed a contradiction in the position of the Schmoller circle (German Historical School). On the one hand, they rejected the positivistic demand for a science of law that was to be built from the historical experiences of society; on the other hand, they believed that economic theory was to be abstracted from economic experiences. It was astonishing to me that this contradiction was barely noticed and rarely mentioned.
It was my intense interest in historical knowledge that enabled me to perceive readily the inadequacy of German historicism. It did not deal with scientific problems, but with the glorification and justification of Prussian policies and Prussian authoritarian government.
Richard was fighting a two-front battle for applied mathematics against the pure mathematicians and the empirically minded fluid dynamicists. He brought together, correctly in my view, strong mathematical approaches to real engineering problems that he faced developing aircraft for the Austrian military during WWI. But like Ludwig, Richard suffered in his professional career because of his methodological approach, as well as other extraneous reasons such as the rise of Hitler.
Indeed, Siegmund-Schultze argues “that von Mises’s contributions to fluid dynamics and aerodynamics suffered chiefly from two somewhat interconnected deficiencies as compared to the work of his principal competitors.”
First, there was von Mises’s methodological preference for applied mathematics as opposed to the reigning hybrid theories of fluid dynamics, which were usually prone to ad hoc adaptation of existing theories to experimental data. … Second, and related to von Mises’s preference for applied mathematics, was his geographical remoteness from the main experimental facilities of fluid dynamics (Aachen, Göttingen) and the data produced there. … Finally, it should not be forgotten that von Mises’s career and posthumous reputation was strongly influenced by his fate as a repeatedly uprooted Jewish scientist.
In the seminal text on fluid dynamics for graduate students by the Cambridge scholar, G. K. Batchelor (the founder and longtime former editor of the prestigious Journal of Fluid Mechanics), he makes no mention of Richard. This is somewhat surprising in that Batchelor was an applied mathematician himself (as students we thought of his book as an applied math text) and often worked with the great experimentalist G. I. Taylor at Cambridge such that “he was a keen advocate of the need for physical understanding and sound experimental basis.”
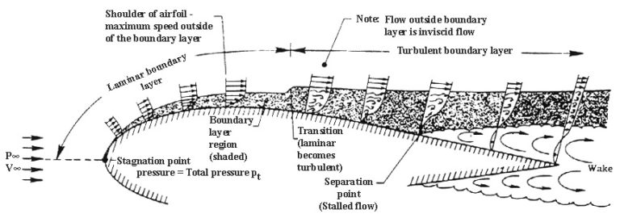
The friendly competitors alluded to above were Theodore von Kàrmàn in Aachen and Ludwig Prandtl in Göttingen; both are seminal developers of fluid mechanics in the 20th century. Von Karman was a student of Prandtl and was a charismatic character on the American scene upon his arrival at Cal Tech in the late 30s. To have a sense of the different approach of Prandtl (boundary layer theory) and von Karman (the explanation of the vortex street) see the images below compared to the image of the metacentric parabola from which Richard developed a new series of airfoils (that were never used in practice).
Prandtl’s boundary layer theory.
Image of a Marman vortex street.
Von Mises’s “metacentric parabola” in von Kàrmàn and Jan M. Burgers, “General Aerodynamic Theory” (ref. 98), plate 2, not mentioning von Mises’s name. From the Siegmund-Schultze article.
Another aspect of independent methodological battles of the brothers was their differing view on the philosophical basis of the Vienna Circle of the Logical Positivists. Richard could be considered a positivist based on this passage from Siegmund-Schultze.
Human Action: The Scho...
Best Price: $6.75
Buy New $15.36
(as of 05:45 UTC - Details)
Generally, one has to be aware of von Mises’s deep-rooted and multifaceted scientific, philosophical, and emotional attachment to his home country, Austria, and above all his reverence for the physicist and philosopher Ernst Mach. Early entries in von Mises’s personal diaries, around 1904, show a permanent occupation with the work of Mach and H. Poincaré. It remains unclear how much of von Mises’s interest then was related to philosophy and, in particular, to positivism and conventionalism. In contrast, in the 1920s, von Mises’s occasional participation in discussions of the Vienna Circle of empiricism philosophy is documented. In 1938, von Mises published a long article on Mach. He also wrote the first textbook on logical positivism in 1939, which was translated into English in 1951.
However, it is confusing to me how this positivism related to his work in fluid dynamics. From Wikipedia logical positivism is “a theory of knowledge which asserted that only statements verifiable through empirical observation are cognitively meaningful.” Yes, to the pure mathematicians, he was soiled by the real world empirical engineering problems he addressed. However, to the empirical fluid dynamicists, his mathematical approach could not capture the reality fluid dynamics problems such as turbulence.
In contrast, Ludwig always battled the positivists in economics. From Last Knight:
Mises later argued along very similar lines that the laws of economics had nothing to do with the acting person’s psychological disposition, but he disagreed with Schumpeter about the nature of economic laws. For Schumpeter, the only basis for scientific propositions was observation of the exterior world. And the only suitable method of economic enquiry was to follow the approach that had proven successful in the natural sciences. In short, he was a positivist who believed that the only method that could yield “facts” was observation of the exterior world. Mises on the other hand followed the program of Menger’s very different “empirical theory” and gathered relevant facts wherever he could find them.
Hulsmann explains further about the intellectual firmament of Vienna.
Such rivalries and disagreements were commonplace, and were not limited to the university. The intellectual organization of early twentieth-century Vienna was a network of dozens of teachers professing their views to disciples and followers in private settings. The system exemplified the intellectual abundance that results from a free market of ideas. It produced Austro-Marxism, psychoanalysis, legal positivism, logical positivism, and praxeology. But for international reputation and lasting impact, three of these circles stood above the rest: the psychoanalysts, the logical positivists, and the Mises Circle.
There is this anecdote of the rivalry between the brothers as told by Hulsmann.
Liberalism
Best Price: $97.99
(as of 04:25 UTC - Details)
He (Ludwig) added an entirely new chapter—the only chapter with no counterpart in Nationalökonomie—to discuss the basic problems of probability theory, which was at the heart of the quantitative approach that dominated economic analysis in the Anglo-Saxon countries. In this chapter, Mises seized the opportunity to build on and elaborate the works of his brother Richard, who had pioneered the so-called relative-frequency theory of probability. Mises considerably simplified the axiomatic exposition of the theory and argued, without mentioning his brother by name, that the standard account was redundant.
Beyond the scholarly aspect of this contribution, the correction of his brother was a sequence in a typical “Austrian” literary squabble. Twelve years earlier, Richard had ventured into the field of his elder sibling, and claimed in one of his books that laissez-faire policies had no scientific merit. Now Ludwig struck back by demonstrating what an elegant exposition of the relative-frequency theory looked like.
Both Richard and Ludwig suffered greatly from Nazi antisemitism. Richard had a sojourn in Istanbul in the 30s, while Ludwig was in Geneva. But Richard ended his career with a post at Harvard while Ludwig had a “visiting” position paid by the Volker Fund for decades at New York University. After the war Richard was honored as shown in the photograph below. Of course, happily Ludwig has a growing following based on the work of Lew Rockwell and the founding of the Mises Institute.
Honorary doctoral degrees by the University of Istanbul to John von Neumann (another giant in the filed), Richard von Mises, and Geoffrey Taylor (front row from left to right), during the Eighth International Congress for Theoretical and Applied Mechanics at Istanbul, Turkey, August 20 to 28, 1952. (Original Source: RVMP, HUG 4574.90P, Courtesy Magda Tisza and Harvard University Archives.) From the Siegmund-Schultze article.
